It’s the time of year for saving money!
Like many other seemingly very simple things, loudspeakers, when you actually stop to look at how they work, aren’t really simple at all: It’s true that, at base, all most speakers really consist of is a motor mechanism and a diaphragm – usually a cone, but it could also be a ribbon, a dome, a panel, or any of a number of other configurations — that gets moved by it in such a manner as to create pressure waves that we hear as sound. And because any sound other than a single pulse consists of a series of waves that alternate back and forth between greater and lesser pressure (positive to negative; negative to positive; negative to more or less negative; positive to more or less positive) the movement of that diaphragm is almost always back and forth, too.
 Still seem simple? Well, keep reading.
Still seem simple? Well, keep reading.
The pattern of “back and forth/greater or lesser pressure” movement is determined by an electrical signal coming to the speaker’s motor mechanism from some source – a microphone, a recording, or even something purely electronic, like a signal generator, for example, or one of the electronic keyboard instruments. And In order to get the signal strong enough to get the diaphragm to move enough to produce pressure waves loud enough to be heard or heard at whatever desired volume level, an amplifier or amplifier-section of some sort is almost always used.
And that’s where things start to get interesting.
One would think that if some reference level of signal were applied to a speaker and it produced one unit of diaphragm movement, then twice that amount of signal would produce twice the movement and half that amount would produce half the movement, and so on. Because decibels (“dB”), the normal way of stating sound pressure levels (“SPL”), are logarithmic, rather than arithmetic, and because perceived volume levels are different from actual power levels (doubling or halving the sound energy will produce a change of 3 dB, but to produce a perceived doubling or halving in loudness requires a change of 10dB, which is either 100 times or 1/100th of the starting energy level, I’m going to try to avoid as much confusion as possible by avoiding, unless it becomes absolutely necessary, the whole issue of decibels in this article and talking, to the degree that I can, only about physical movement.] That can certainly be true, but it’s NEVER true, in actuality, across the entire range of movement of the diaphragm.
 There are a number of reasons for this, some physical, and some electrical, which may involve both the speaker (Let’s, from this point on, be more specific and call it the “driver”) and also the amplifier. In cone drivers, which are certainly the most common type we use, the cone is moved by the magnetic attraction or repulsion of a “voice coil” attached to the cone (it’s the same with domes, and the diaphragms of the compression drivers used for horns). This is mounted within the “gap” of a magnetic structure which is part of the driver, and is powered by the audio signal and changes electromagnetic polarity with the changing polarity of the signal. As the coil is either attracted or repelled by the magnet structure, it causes the cone (or other diaphragm element) to move forward or back, with the driving force for doing so being controlled by both the frequency (how and how often the polarity of the signal changes) and the amplitude (how MUCH it changes) of the signal.
There are a number of reasons for this, some physical, and some electrical, which may involve both the speaker (Let’s, from this point on, be more specific and call it the “driver”) and also the amplifier. In cone drivers, which are certainly the most common type we use, the cone is moved by the magnetic attraction or repulsion of a “voice coil” attached to the cone (it’s the same with domes, and the diaphragms of the compression drivers used for horns). This is mounted within the “gap” of a magnetic structure which is part of the driver, and is powered by the audio signal and changes electromagnetic polarity with the changing polarity of the signal. As the coil is either attracted or repelled by the magnet structure, it causes the cone (or other diaphragm element) to move forward or back, with the driving force for doing so being controlled by both the frequency (how and how often the polarity of the signal changes) and the amplitude (how MUCH it changes) of the signal.
That STARTS, the diaphragm moving, but what STOPS it? Remember, there IS inertia, and an object (the diaphragm) once started moving, will, unless it’s stopped, tend to keep moving forever.
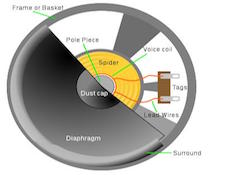
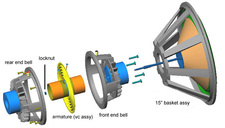 Part of the answer to this question will always be the changing polarity of the incoming signal which, when it reverses polarity acts to resist movement already initiated, but the rest, at least for a cone driver, will be the “spider” – the flexible “accordion-pleated”, often treated-cloth or paper, structure that centers the cone from just above the voice-coil and limits its motion, either forward or backward – and the “surround” – the also-flexible, rolled or accordion-pleated structure at the large end of the cone that, again like the spider, centers it and limits it travel. The surround may also be made out of various materials, including cloth, paper, and either foamed or molded rubber, and has the additional purpose of forming an air-tight seal between the front and back of the cone.
Part of the answer to this question will always be the changing polarity of the incoming signal which, when it reverses polarity acts to resist movement already initiated, but the rest, at least for a cone driver, will be the “spider” – the flexible “accordion-pleated”, often treated-cloth or paper, structure that centers the cone from just above the voice-coil and limits its motion, either forward or backward – and the “surround” – the also-flexible, rolled or accordion-pleated structure at the large end of the cone that, again like the spider, centers it and limits it travel. The surround may also be made out of various materials, including cloth, paper, and either foamed or molded rubber, and has the additional purpose of forming an air-tight seal between the front and back of the cone.
Unless the spider and the surround are designed to be “limp” (as they might be in an “acoustic- suspension” speaker design) they will act like springs, to slow and ultimately limit the cone’s (or other diaphragm’s) motion. And, like all other ordinary springs (not including those that may be specially-designed, of special materials, or “progressively” wound to do otherwise) they will act in accordance with “Hook’s Law”, and exert a resistive force directly proportional with their change in physical dimension. Put most simply, this means that the more distance of movement there is to stretch the spider or the surround, the greater the spring tension will be; with twice the stretch always producing exactly twice the tension.
Now consider this: although the spring effect available to slow and ultimately stop the diaphragm varies arithmetically with the stretch of the spider and the surround, the amount of force necessary to stop the diaphragm so that it can be turned around and started in the opposite direction is NOT arithmetic. It is exponential, and depends on just two things; the MASS of the diaphragm and other moving parts (the voice coil and the moving portions of the spider and surround), all of which remain constant; and the velocity at which they are moving when they need to be stopped and turned around.
 The higher the frequency, the more times the diaphragm will move back and forth per second; the louder the signal, the FARTHER it will move back and forth per second. That means that either a higher frequency or a louder one (or both) can make the diaphragm move a greater total distance in any second, and thereby cause it to travel at a higher velocity. With the effect of velocity being exponential (Four times for each doubling) rather than arithmetic, (Only twice for each doubling) it must be obvious that the effect of velocity is by far the more important. It must also be apparent that, with the power to control the diaphragm increasing far less than the need to control it, the greater the velocity of the diaphragm becomes, the less control for it is available.
The higher the frequency, the more times the diaphragm will move back and forth per second; the louder the signal, the FARTHER it will move back and forth per second. That means that either a higher frequency or a louder one (or both) can make the diaphragm move a greater total distance in any second, and thereby cause it to travel at a higher velocity. With the effect of velocity being exponential (Four times for each doubling) rather than arithmetic, (Only twice for each doubling) it must be obvious that the effect of velocity is by far the more important. It must also be apparent that, with the power to control the diaphragm increasing far less than the need to control it, the greater the velocity of the diaphragm becomes, the less control for it is available.
One of the most significant results of this is “dynamic compression”. That’s what I’ll write about next time.
I hope to see you then.