It’s the time of year for saving money!
In the last installment (Part 5) of this continuing series, after briefly summarizing all that had gone before, including the coming of stereophonic sound to the home entertainment market and some of the new problems it created, I went on to write about stereo’s big trick — letting the listener know the specific location of each and all of the, often moving, sources of the recorded sound. To do that, I said, one of the most basic requirements is for all of the sound from all of the drivers of each of the two stereo speakers to reach the ears of the listener at the same time.
 Big steps toward achieving that, I said, had been made by lining up the centers of all of the drivers of each speaker on a single vertical plane to form a “line source”. Other positive steps, I said, had been made by adjusting the front-to-rear positioning of the drivers so that all of their voice coils lined-up on a single plane (to achieve “time-alignment”); by positioning the woofer and tweeter of a two-way system concentrically (at least aligning their centers and, depending on the specific design, possibly also aligning their voice coils), or, most simply, by just going to a single full-range (probably planar) speaker system per stereo channel.
Big steps toward achieving that, I said, had been made by lining up the centers of all of the drivers of each speaker on a single vertical plane to form a “line source”. Other positive steps, I said, had been made by adjusting the front-to-rear positioning of the drivers so that all of their voice coils lined-up on a single plane (to achieve “time-alignment”); by positioning the woofer and tweeter of a two-way system concentrically (at least aligning their centers and, depending on the specific design, possibly also aligning their voice coils), or, most simply, by just going to a single full-range (probably planar) speaker system per stereo channel.
Any of those things would go a long way toward ensuring correct arrival time at the listener’s ears but, except for speaker systems that use just one full-range driver – which don’t need them, anyway — they probably can’t do anything about another type of “arrival-time” problem; “phase-shift” between the various frequencies that make up the music or other signal.
I told you last time that the relative phase of the sounds reaching our two ears is one of just three clues (relative amplitude, relative arrival time, and relative phase) available to us for “triangulating on” and locating the source of the sounds we hear. In starting to explain this, I reminded you that sound is a series of alternating higher and lower pressure zones that moves through the air and radiates in all directions from whatever vibrating object is producing it; that one high pressure zone plus one low pressure zone makes one complete waveform; that each of the two halves (the pressure zones) of a waveform is called a “phase” and that each phase is divided into 180 degrees. I also told you how to calculate the wavelength of any frequency by simply dividing it into the speed of sound at sea level. (around 1100 feet per second, depending on ambient air temperature and pressure). Then, referring to the fact that the “typical” distance between a person’s ears is about 5 inches [12.7 cm], I showed you how that 5 inch distance equals 1 complete wavelength (360 degrees of phase) for a tone of about 2.6 kHz and a DIFFERENT number of whole or fractional wavelengths or degrees of phase for every other frequency.
 Although I told you that those frequency-related differences were of major importance and could result in “a ‘smearing’ of stereo images, especially in the critical mid- and upper frequencies, with a corresponding loss of locational information”, I didn’t at that time explain how or why that might happen. Well, here’s that explanation now:
Although I told you that those frequency-related differences were of major importance and could result in “a ‘smearing’ of stereo images, especially in the critical mid- and upper frequencies, with a corresponding loss of locational information”, I didn’t at that time explain how or why that might happen. Well, here’s that explanation now:
Although it’s both convenient and common for us to talk in terms of single frequencies – the 440Hz “A”, for example, which (except by advocates of 432Hz) is generally accepted as the tuning standard for musical instruments – the fact is that other than the tones produced by an electronic signal generator or a specially-designed mechanical tuning fork, single tones almost never occur, either in nature or in music. EVERYTHING has a “fundamental” resonant frequency at which it will vibrate when stimulated, and almost everything will also vibrate at multiples (harmonics) of that frequency. For that 440 Hz tone just mentioned, 440Hz may be called either the “fundamental” or the “first harmonic”; 880Hz (twice 440) is the “second harmonic”; 1320Hz (three times 440) is the “third harmonic”, and so on, often extending to, or even beyond the limits of human hearing. Musical instruments are devices that are designed and specifically intended to add harmonics (especially “even order” ones, which people generally find pleasing) to whatever tone they are playing, with the presence and amplitude of those harmonics dependent on the design and materials of the instrument, the musical note being played, and the proximity of the frequency of that note to the fundamental resonance of the instrument, itself. That’s why a 440 “A” played on a piano, a violin, a clarinet, or a trombone are all exactly the same note, but all sound totally different.
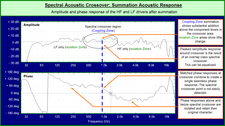 It’s also why it’s not at all uncommon for a tone whose fundamental is reproduced by one driver of a speaker system to have its harmonics reproduced by another. Bass tones, for example, whose fundamentals are played by the speaker’s woofer, quite often have harmonics played on the mid-range driver and (depending on the instrument and the tone being played and the nature, number of drivers, and crossover frequency or frequencies of the speaker that the tone is being played on)
may even have upper harmonics played by the tweeter, too. Something with a very sharp dynamic
”attack” and a quick “rise time” could certainly fall into that category.
It’s also why it’s not at all uncommon for a tone whose fundamental is reproduced by one driver of a speaker system to have its harmonics reproduced by another. Bass tones, for example, whose fundamentals are played by the speaker’s woofer, quite often have harmonics played on the mid-range driver and (depending on the instrument and the tone being played and the nature, number of drivers, and crossover frequency or frequencies of the speaker that the tone is being played on)
may even have upper harmonics played by the tweeter, too. Something with a very sharp dynamic
”attack” and a quick “rise time” could certainly fall into that category.
And THAT’s where the problem lies: Everything other than a true full-range single driver speaker system requires a crossover network to send the right frequencies to the right driver and, as I wrote last time, “The problem for speaker designers is that phase information is strongly frequency-related AND SO IS THE CROSSOVER FUNCTION OR FUNCTIONS THAT “SORT OUT” WHICH FREQUENCIES GO TO WHICH OF A SPEAKER’S DRIVERS. Even a simple “two-way” system, with just a woofer and a tweeter requires one crossover network. A “three-way” system, with a woofer, a midrange, and a tweeter, requires two; and another must be added for each additional frequency band and driver. What makes that a problem is that a conventional crossover network imposes 90 degrees of “phase-shift” (time MIS-alignment distortion) for each 6dB of attenuation PER OCTAVE per octave after its crossover frequency. (A “First Order” crossover attenuates (“rolls-off”) unwanted frequencies at 6dB per octave; a “Second Order” crossover rolls them off at 12 dB per octave; a “Third Order” crossover at 18dB per octave, and so on) The result is that, even with just a single crossover network (and remember that there can be two or more) THE FREQUENCIES OF A SINGLE INSTRUMENT CAN BE SPREAD ACROSS MULTIPLE DRIVERS AND CAN BE PHASE-SHIFTED (depending on the instrument’s harmonic structure; which harmonic we’re talking about; and the “order” of the crossover) ANYWHERE FROM JUST A FEW DEGREES TO SEVERAL FULL WAVEFORMS, changing and spreading that instrument’s apparent size, shape, and location significantly enough that quite convincing artificial stereo systems have been created using nothing more than just phase-shift, time delay, and, occasionally, a little frequency “shaping”.
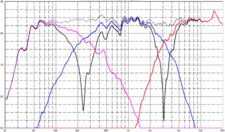 There ARE, however, things that can be done to overcome problems of phase-shift, even if the conventional solutions of driver-placement and time-alignment get undercut by crossover problems.
The first and simplest thing, of course, would just be to come up with true full-range single driver speaker systems that don’t require any crossover at all. Although difficult and expensive, that could be done. Another “fix” is already being seen in the form of phase-correct digital crossovers for use with bi-, or even multiply-amped systems, or in digital devices that that can not only correct phase-shift, but room acoustics, as well.
There ARE, however, things that can be done to overcome problems of phase-shift, even if the conventional solutions of driver-placement and time-alignment get undercut by crossover problems.
The first and simplest thing, of course, would just be to come up with true full-range single driver speaker systems that don’t require any crossover at all. Although difficult and expensive, that could be done. Another “fix” is already being seen in the form of phase-correct digital crossovers for use with bi-, or even multiply-amped systems, or in digital devices that that can not only correct phase-shift, but room acoustics, as well.
I’ll write a little about those next time.
See you then!