It’s the time of year for saving money!
As discussed in my last installment, one approach to digitizing an analog signal is to divide the analog waveform into so many thousands of slices per second and, for each slice, to record the amplitude of the waveform number, or integer, ranging from 0-N.
 More because of the computer processors and chips used when CD’s emerged than anything else, that number was stored as a 16-bit “word“, giving it of a range of 0-65535. While this seems like a very large span, the actual dynamic range associated with the span depends of how much of a difference in voltage one assigns to each next bigger integer when converting the numbers back into an analog signal in a DAC. Of course, these values are standardized. They must be.
More because of the computer processors and chips used when CD’s emerged than anything else, that number was stored as a 16-bit “word“, giving it of a range of 0-65535. While this seems like a very large span, the actual dynamic range associated with the span depends of how much of a difference in voltage one assigns to each next bigger integer when converting the numbers back into an analog signal in a DAC. Of course, these values are standardized. They must be.
By convention, the maximum dynamic range associated with a 16-bit word, or value from 0-65535, equals about 96 dB, the threshold of pain for human hearing equaling about 120 dB. Something called dither, itself a form of deliberate noise in the digital domain, can hypothetically increase the perceived dynamic range of a 16-bit word to about 120 dB. However, dither is a tricky thing and, not unlike lossy compression used in MP3 files, doesn’t always fool human hearing as readily as some research would indicate.
A simple way to give you more dynamic range is to increase the word size from 16 to 24 bits, increasing the span of integer values to 0-16,777,215. or a true 144 dB. Given two identical digital files sampled at, say, 44.1 kHz, one using 16-bit words and the other using 24-bit words, the latter may sound better simply you have a greater actual difference between the softest and loudest reproducible passages of music given only 8 more bits, or 0’s and 1’s, per sample / slice.
The last installment also discussed the Nyquist theorem and how, at sampling rate of 44.1 thousand slice per second, or kHz, you should be able to cover the range of human hearing from 20-20kHz. Think about it though. If you’re in a city late at night and you hear a siren in the distance, it may be at 60 dB below a nominal 0 dB, but you can still hear it. In that same sense, you may not be able to hear a 40-kHz musical overtone as loudly as you hear a 20-kHz overtone, but that doesn’t mean you can’t perceive it and that it doesn’t affect your interpretation of or emotional reaction to the music.
A sampling rate of 96-kHz gives you the ability to store up to about a 48-kHz musical overtone; and a 192-kHz sampling rate gives you a whopping upper audible frequency of about 96 kHz. Combine a 24-bit word with a 192-kHz sample rate, and you end up with a kind of a digital envelope capable of storing sound from 0-144 dB at anywhere from 0-96kHz. That’s a mighty big envelope, and does not require perceptual tricks, like dithering, to fool you into thinking you hear more music than is in the metaphorical envelope.
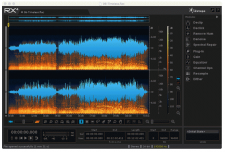 Using iZotope RX4–of the title track (left channel above right channel) from John Abercrombie’s album Timeless at 24/192 PCM. As you can see, the musical information easily reaches close to 50-kHz and the dynamic range, expressed as contrasting colors, appears quite dramatic, ranging from 0 to nearly 120 dB.
Using iZotope RX4–of the title track (left channel above right channel) from John Abercrombie’s album Timeless at 24/192 PCM. As you can see, the musical information easily reaches close to 50-kHz and the dynamic range, expressed as contrasting colors, appears quite dramatic, ranging from 0 to nearly 120 dB.
I should make it doubly clear that, right now, we’re only discussing PCM-based approaches to DSP, not DSD, also known as single-bit or, sometimes, Delta-Sigma modulation. The former looks at amplitudes in chucks with a range from 0-N. The later looks at the analog waveform one bit at a time and uses various techniques to indicate if a single 0 or 1 means:
- Increase the amplitude a little
- Decrease the amplitude a little
- Leave the amplitude the same
The Nyquist theorem still applies and you still divide the analog waveform into thousands of slices, the difference being how many bits you can associate with a slice, 16, 24, or just 1, and what that implies when decoding the series of numbers back into an analog signal or waveform. Of course, the interval, or time, between slices must be very precise and as digital technology progresses ADC’s and DAC’s get more and more accurate oscillators or clocks for measuring this interval.
Plus, as mentioned before, some devices have the ability to all be synced by a master clock so whatever timing errors occur are exactly the same in all devices, although, oddly, enough, no consumer digital media carry a clock signal that could be supplied by the ADC and used by the DAC to reproduce the exact interval between samples even when minor timing errors occur during encoding, such errors generally referred to as “jitter“. In professional recording devices, like the Sound Devices 702T digital field recorder, you get three tracks, left, right, and something called timecode, a clock signal, just to keep recording and playback in sync.
 One comment I should make is that, as sophisticated as the term “Delta-Sigma” sounds, it’s just a compound noun where, in mathematics, Delta means change and Sigma means sum or total. So, simply put, Delta-Sigma just means change in sum or total [amplitude], and, as such, refers to the same type of measurement taken in PCM, but, in DSD, using single bit values as opposed to multi-bit values, not even necessarily at a higher sample rate than used in PCM. This reaches beyond marketing hype to the level of consumer electronics propaganda, IMHO. However, I mean no harsh criticism except to say … more on DSD (Direct Stream Data) later.
One comment I should make is that, as sophisticated as the term “Delta-Sigma” sounds, it’s just a compound noun where, in mathematics, Delta means change and Sigma means sum or total. So, simply put, Delta-Sigma just means change in sum or total [amplitude], and, as such, refers to the same type of measurement taken in PCM, but, in DSD, using single bit values as opposed to multi-bit values, not even necessarily at a higher sample rate than used in PCM. This reaches beyond marketing hype to the level of consumer electronics propaganda, IMHO. However, I mean no harsh criticism except to say … more on DSD (Direct Stream Data) later.
Unlike the kind of analog distortion that occurs when you overload a signal and get a kind of crunching sound, overloading the input of an ADC results in a catastrophic event and, put metaphorically, the bits just go crazy. So, it’s even more important when using an ADC to encode an analog recording to keep the peak amplitudes low and/or use something called a peak limiter, which generally works in the analog domain and quickly hammers down on any voltage spikes in the analog signal above a preset point to keep the ADC from running amok.
In the same sense, any analog frequencies more than about 2 times the sampling rate (referring again to the Nyquist theorem) cause a catastrophic digital failure so, if you’re recording at 48 kHz, you must use a low-pass or “brick wall” filter to eliminate the analog signal passing above 24 kHz. The problem is that filtering of any kind, either in the ADC or DAC, cause its own form of distortion usually in the time or “phase” domain problems (see below).
 Some DAC’s, like those from Audio Note, don’t use any explicit output filtration and just send a quasi-square wave to your amp, but they usually send the resultant analog signal through capacitors, transformers, and/or vacuum tubes first, which tend to naturally smooth out the square wave a little and create a more sinusoidal form.
Some DAC’s, like those from Audio Note, don’t use any explicit output filtration and just send a quasi-square wave to your amp, but they usually send the resultant analog signal through capacitors, transformers, and/or vacuum tubes first, which tend to naturally smooth out the square wave a little and create a more sinusoidal form.
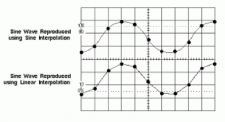
Lastly, oversampling and interpolation should not be confused. Oversampling simply means that your DAC operates at a higher clock speed or frequency than your ADC, resulting in multiple occurrences of the same integer value associated with each ADC time slice, such as “04, 04, 04” versus simply “04”. You get no more resolute information.
Interpolation, a form of DSP rarely used in consumer audio, increases the number of actual points of information than those originally sampled making educated guesses about what said values would be based on, for example, simple averages, so an interpolated series of integers starting with “02, 04, 08” could lead to “02, 03, 04, 06, 08”, creating a more densely packed square wave with more actual points or slices of information that could be more readily smoothed into a sinusoidal, or musical, shape with less output filtering and thus less phase distortion.
Interpolation and extrapolation are common mathematical techniques used, in one case, to calculate the value of Absolute Zero (minus 459.67 degrees Fahrenheit or minus 273.15 degrees Celsius), the temperature at which the movement of atoms would stop, without it being measured empirically or observationally. Next time, we get back to more music …