It’s the time of year for saving money!
 So you know how it goes; there’s the HiFi Crazies on one side, who say that cables DO make a difference; that that difference is clear and obvious; and that anybody who can’t (or WON’T) hear it must be either deaf, have his head up his butt (If you put it up far enough, your ears get dirty and you can’t hear very well), or must be some kind of damn fool or troll.
So you know how it goes; there’s the HiFi Crazies on one side, who say that cables DO make a difference; that that difference is clear and obvious; and that anybody who can’t (or WON’T) hear it must be either deaf, have his head up his butt (If you put it up far enough, your ears get dirty and you can’t hear very well), or must be some kind of damn fool or troll.
And on the other side, there’s the damn fools and trolls who say that HiFi Crazies are crazy; that they believe in snake oil, voodoo, and other batsh*t nonsense, and that they should all finally wise-up and accept that, regardless of what they THINK they hear, cables depend not at all on exotic designs and exotic materials; are affected by nothing other than resistance (“R”), capacitance (“C”), inductance (“L”), and characteristic impedance (“ZO”); and ― if they’re “properly” designed and built ― don’t affect the sound at all.
I’ve already written two articles (“One Down” and “Two Down“) on the “fab four” – the conventional cable parameters, R, C, L, and ZO – and have shown, at least to the satisfaction of some goodly portion of my readers, that, for audio purposes, resistance and characteristic impedance are either of little consequence, are easily dealt with, or are utterly irrelevant. Capacitance, though, is a different matter, entirely: It really IS of great consequence, to cable performance as to so many other areas of electronics, and its nature is such that it might very well provide the perfect proof to those out there who so gleefully brandish pitchforks and cry “Voodoo!” that there’s more to how cables work than they’ve ever imagined or been willing to admit.
For one thing, cables don’t just HAVE capacitance; for all practical purposes, they actually ARE capacitors and, depending on their specific design, might actually be as many as several different capacitors in a single deceptively simple-seeming structure.
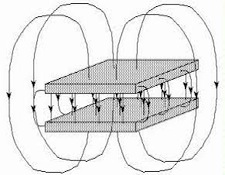 To understand how that’s possible, consider this: In the final analysis, all any capacitor is is a system of two conductors (the “plates”) separated by a non-conductor (the “dielectric”), such that when a voltage is applied to the plates, it stores or releases energy. When more conductors are added – each separated from the others by a dielectric, and each with its own separate charge source (in short, NOT just more wires of the same circuit) more capacitors will be created, one for each possible combination. (two wires can only make one capacitor [A+B]; three wires can make three capacitors [A+B, A+C, C+B], four wires can make six capacitors [A+B, A+C, A+D, B+C, B+D, D+C], and so on, with the perfect three-wire example being a two-conductor shielded cable, which really DOES [Go ahead and COUNT ’em] have all three capacitors present and even has the possibility of a fourth one that I may touch on in some future article.
To understand how that’s possible, consider this: In the final analysis, all any capacitor is is a system of two conductors (the “plates”) separated by a non-conductor (the “dielectric”), such that when a voltage is applied to the plates, it stores or releases energy. When more conductors are added – each separated from the others by a dielectric, and each with its own separate charge source (in short, NOT just more wires of the same circuit) more capacitors will be created, one for each possible combination. (two wires can only make one capacitor [A+B]; three wires can make three capacitors [A+B, A+C, C+B], four wires can make six capacitors [A+B, A+C, A+D, B+C, B+D, D+C], and so on, with the perfect three-wire example being a two-conductor shielded cable, which really DOES [Go ahead and COUNT ’em] have all three capacitors present and even has the possibility of a fourth one that I may touch on in some future article.
In the most basic complete cable, just two conductors ― one “hot” and one “ground” ― allow the completion of a circuit and, because we know that’s true, we can be certain that the conductors never touch, either each other or any common conductor anywhere along their length. (If they did, a “short” in the circuit would prevent the passage of signal.) Not touching means that there’s a non-conductive (or at least effectively non-conductive) distance between them, and that distance ― whether or not there’s anything in it ― acts, in every case, as a dielectric to (voila!) create a capacitor!
If that cable just mentioned were out in space, in a satellite, for example, or on the outside of the International Space Station, and if its wires were just two bare wires, the dielectric – the stuff occupying the space between them – would be “hard” vacuum and would, as the dielectric material LEAST able to store energy, be said to have a dielectric constant of “1”. Any other material would have a greater energy storage capacity for any identical volume of material and its dielectric constant would be the number indicating how much greater that capacity was. A material that could store 4.7 times as much energy as an equal volume of vacuum would, for example, have a dielectric constant (commonly written as the letter “K”) of 4.7.
]]> Air, the material most beloved by cable designers (including me) as the dielectric for their cables, has a K of around 1.0006 at sea level, just ― because for cables you want the lowest K possible – a little worse than a vacuum. Balsa wood, which designer Knut Skogrand uses as part of the dielectric of his “Skogrand” cables, has a K of 1.4; the K of the various varieties of Dupont® Teflon® runs from 1.95 to around 2.1; Polyethylene (another good cable dielectric) has a K of around 2.2; and the K of PVC (polyvinyl chloride) ― by far the most common of all dielectric and insulating materials for cable use ― ranges, depending on the kind and amount of plasticizers that have been mixed-in with it, from around 3.5 to as high as around 7.0!
Air, the material most beloved by cable designers (including me) as the dielectric for their cables, has a K of around 1.0006 at sea level, just ― because for cables you want the lowest K possible – a little worse than a vacuum. Balsa wood, which designer Knut Skogrand uses as part of the dielectric of his “Skogrand” cables, has a K of 1.4; the K of the various varieties of Dupont® Teflon® runs from 1.95 to around 2.1; Polyethylene (another good cable dielectric) has a K of around 2.2; and the K of PVC (polyvinyl chloride) ― by far the most common of all dielectric and insulating materials for cable use ― ranges, depending on the kind and amount of plasticizers that have been mixed-in with it, from around 3.5 to as high as around 7.0!
One thing that must be remembered is that ALL of the materials in the space between the plates of a capacitor (On the two wire example, this could be Teflon insulation on one wire, PVC on the other, and air in a space between them) contribute to the capacitor’s total dielectric, becoming, effectively, a single composite dielectric material. It is the dielectric constant of this “composite material” that determines how much energy any given volume of it will be capable of storing, and it is how much of the composite material is actually present, and in what configuration, that determines a capacitor’s total storage capability (its “capacitance”), which is usually stated in micro-, nano-, or picofarads (millionths, billionths, or trillionths of a Farad – a unit named after 19th century scientist Michael Faraday, who did much of the basic research on capacitors).
Now consider this: There are at least a dozen different dielectric materials used in commercial capacitors and, when you add-in all of the other things (fillers, spacers, decorative braid, etc.) that can be added in the construction or use of cables, and all of the possible combinations of material, thickness, and proximity (within the cable, itself, and to other cables) that can go into the makeup of a cable’s overall composite dielectric, the number of possible effective dielectric constants becomes effectively infinite.
 Here’s where it gets tricky: Even though all the numbers boys tell us that capacitance is one of the determining factors in cable design they (HERE IT COMES: TROLLS GET OUT YOUR NOTEPADS AND LIMBER-UP BOTH OF YOUR TYPING FINGERS) overlook the fact that any given amount of capacitance – 10 microfarads, for example – can be produced by, literally, THOUSANDS of different composite dielectrics and that each one of those will not only have a different K, but will also have a different charge rate; a different discharge (“dump”) rate; a different dissipation (or “power” or dielectric absorption) factor; a different “ESR” (“equivalent series resistance”) and any number of other factors that – for a commercial capacitor ― can affect its performance and suitability in any given application and ― for a cable ― can affect its sound.
Here’s where it gets tricky: Even though all the numbers boys tell us that capacitance is one of the determining factors in cable design they (HERE IT COMES: TROLLS GET OUT YOUR NOTEPADS AND LIMBER-UP BOTH OF YOUR TYPING FINGERS) overlook the fact that any given amount of capacitance – 10 microfarads, for example – can be produced by, literally, THOUSANDS of different composite dielectrics and that each one of those will not only have a different K, but will also have a different charge rate; a different discharge (“dump”) rate; a different dissipation (or “power” or dielectric absorption) factor; a different “ESR” (“equivalent series resistance”) and any number of other factors that – for a commercial capacitor ― can affect its performance and suitability in any given application and ― for a cable ― can affect its sound.
So here’s the question: If everybody (even the EEs and the AES members), agrees that differing capacitors ― even of exactly the same value and (let’s toss this one in, just for fun) the same “working voltage” ― are different enough and affect performance enough that they will specify not just a value, but a KIND of capacitor for their electronics and, especially, their crossover designs, why won’t they also agree that the capacitors called “cables” are different, too, and can affect the sound of a system just as much as other capacitors can affect the performance of other things?
Come on, trolls, dive in!
Does that make three down?